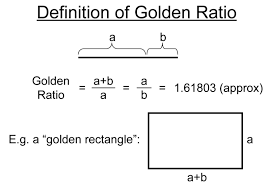
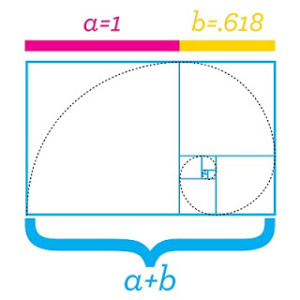
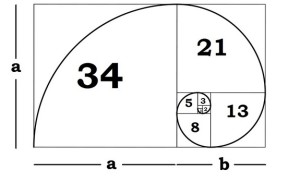
The Golden Ration is found in the Fibbonaci Sequence
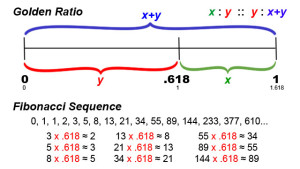
Fibonacci Number Formula
The Fibonacci numbers (Fn) are generated by setting F0=0, F1=1, and then using the recursive formula
Fn-1 + Fn-2 = Fn
0+1= 1, 1+1= 2, 1+2= 3, 2+3= 5, 3+5= 8 and so on…
Every consecutive number is the sum of the two preceding numbers
0,1,1,2,3,5,8,13,21,34,55,89,144 … = 1.618 … Φ
This sequence of Fibonacci numbers arises all over mathematics and also in nature
The Fibbonaci osilates above and below The Golden Ratio but not quite reaching it – This goes on for Infinity